The 10x Rule: Analysing the Relationship Between Budget and Worldwide Gross in Movies

Outside of my passion in football, there is a close second in films. I love going to the cinema and I also enjoy watching a movie on my sofa every Sunday evening after the 16:30 Super Sunday kick-off.

Despite my extensive catalogue of football podcasts, I only listen to one for movies and that is the Movies You Forgot You Forgot podcast hosted by Joe Devine (from Tifo football) and Adam Richmond.

The premise is rather simple - they watch and discuss films that they had forgotten they had even seen in the first place. The show is full of fun games, one of which is called “The Box Office Game”, here Adam has to guess the budget, the US opening weekend gross, and the worldwide gross that the film makes. A recent development in the pod has been the hotly contested “10x rule” which Joe states: roughly speaking, the average worldwide gross return is 10x the budget. He relates this to xG, in that movies can over/under-perform their 10x rule and this is indicative of the movie’s performance.

Being the massive football/data nerd that I am, this got me thinking: I wonder how this rule would stand up statistically? And this is what this post will try to answer.

By the way, if you like films at all, I would strongly recommend checking out the podcast - it is my favourite listen each week!

---

My first step was to seek out a database which had as many movie releases as possible and their budgets and worldwide gross returns. The best source I found was at The Numbers, the dataset I obtained has over 6,000 movies and includes the release date, the production budget, the domestic gross (US), and the worldwide gross. I could have sought out more data per movie, something like genre and director would have been interesting to include too - but given the quality of this less dimensional dataset, I decided to stick with it.

I removed any movies that had no worldwide gross (i.e. straight to streaming/DVD) and movies with less than $10k worldwide gross. I also took out any movies with missing release dates.

My approach was to fit a Linear Regression model, which is essentially setting a line of best fit through the target variable and an explanatory variable (when using one feature that is). This assumes that the relationship between budget and worldwide gross is linear, which in this case appears to be approximately true and for our purposes here, it is a reasonable model given we are looking for interpretability over model prediction accuracy.

---

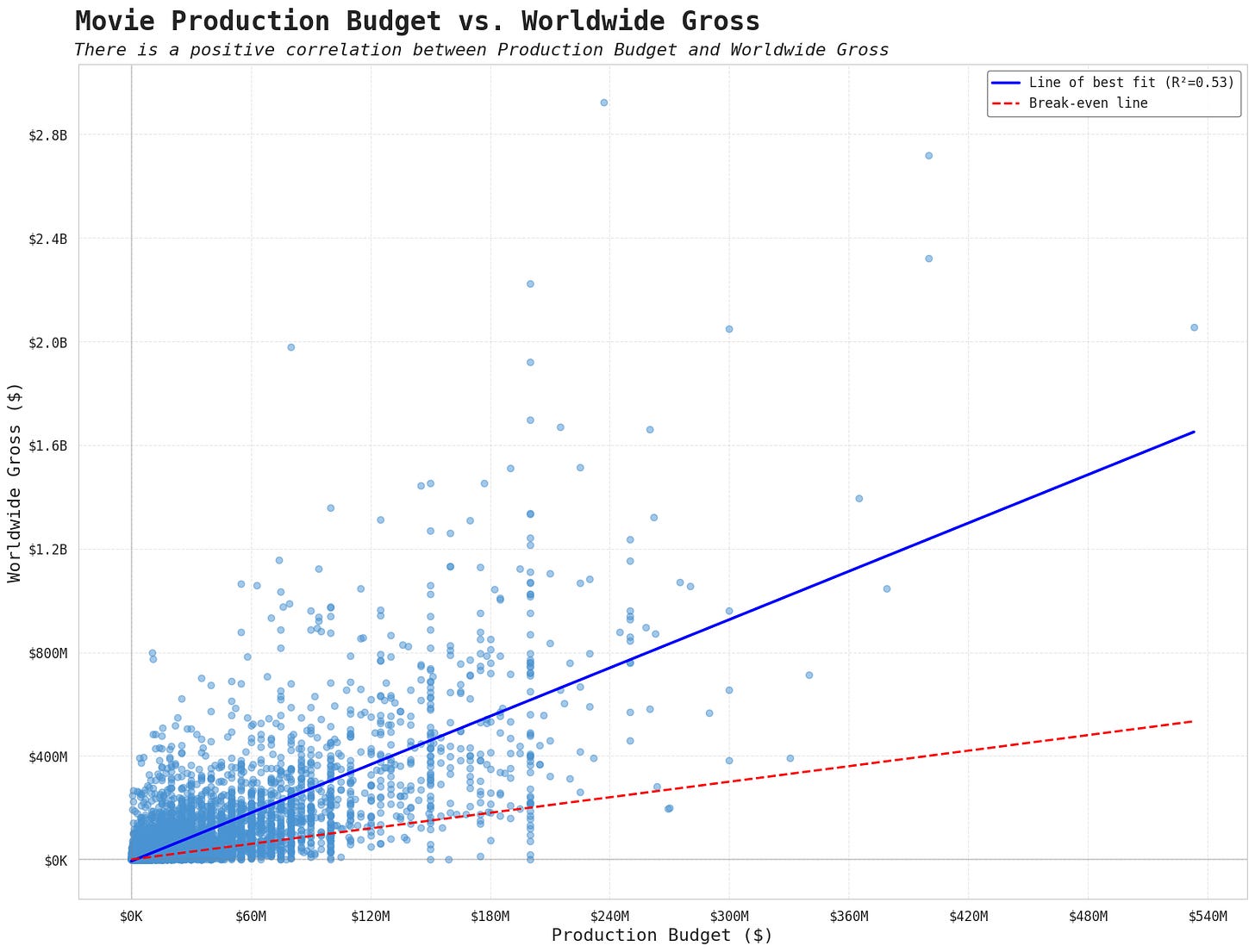
So, looking at univariate linear regression to begin with: only considering the production budget and worldwide gross, we can see a distinct positive relationship. The red dotted line represents where films would break-even, the blue line represents the line of best fit, and the result of the linear model. We can see a stronger positive relationship than the red dotted line which tells us that increasing budget tends to increase return of investment by a considerable amount over breaking even.

The OLS regression method was used here, and when analysing the statistical results we can see that the R-squared value is 0.53 meaning that 53% of the variance in worldwide gross is explained by the production budget, a good amount for only looking at one variable. Looking further at the coefficient of the production budget in the model, it has a statistically significant effect and a value of 3.11, this means that for every $1M increase in budget you can expect, on average, a $3.11M increase in worldwide gross.

So, these results suggest that the 10x rule might be better named the 3.11x rule - although, it doesn’t exactly have the same ring to it. It’s also worth considering that the films covered on the pod are generally relatively mainstream - films that are worth covering, and this dataset includes a whole range of different films, including many that I imagine 99% of people would have never heard of in their lives. Therefore, I think it’s fair to assume that this rule would be inflated when only considering the films that are on the pod.

---

Despite getting reasonable results from only looking at production budget as an explanatory variable, I wanted to get further into the weeds. I next looked at including release date.

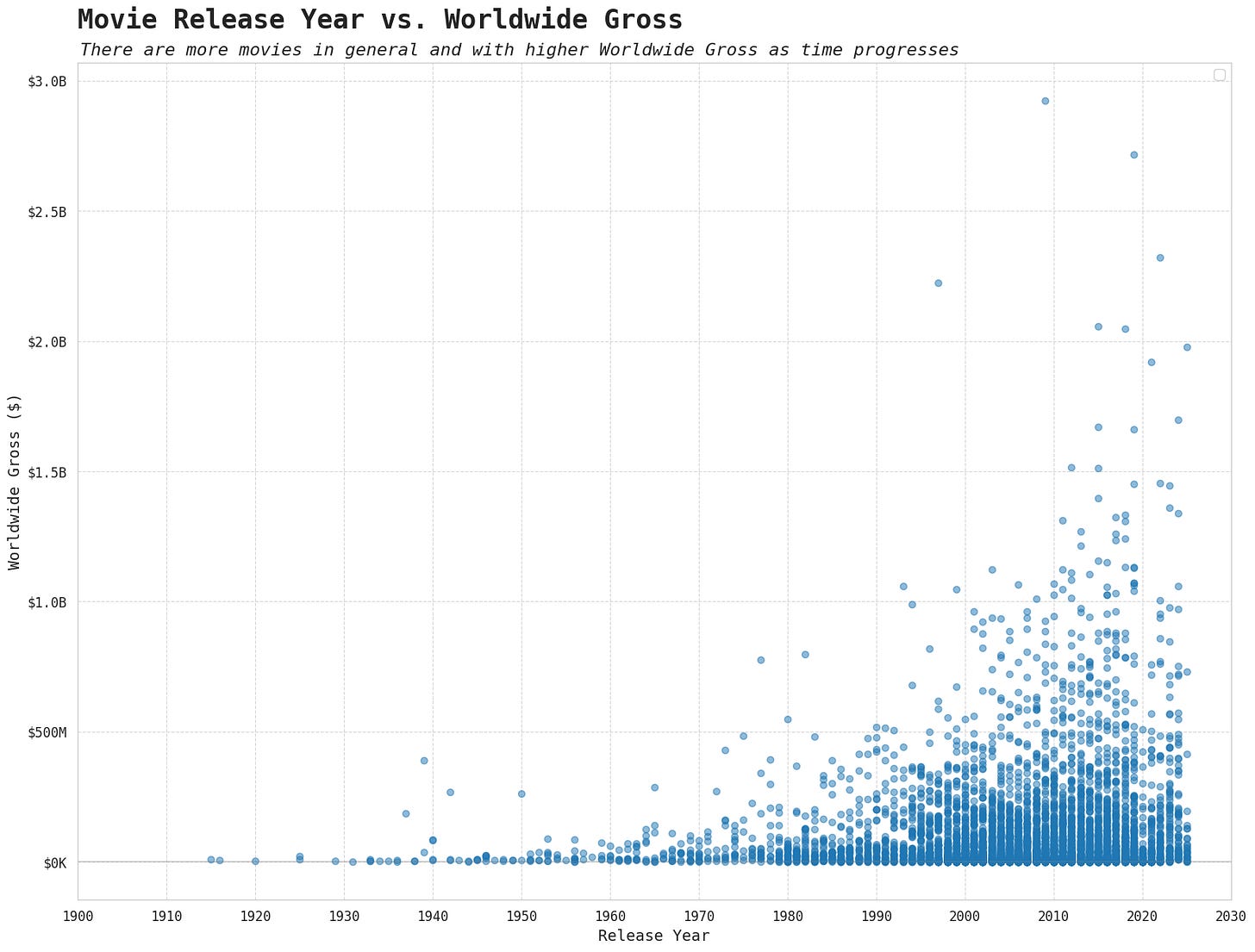
I broke this down into two variables: release year and release month. As you can see from the chart below, more movies get released each year as time progresses and there are more movies with higher worldwide gross. I wouldn’t necessarily say there is a linear positive relationship though, as there continues to be lots of low return movies in the 2020s. After some experimentation, I decided to include release year as a quadratic term as the relationship was nonlinear and there was a very minor U-shape present.

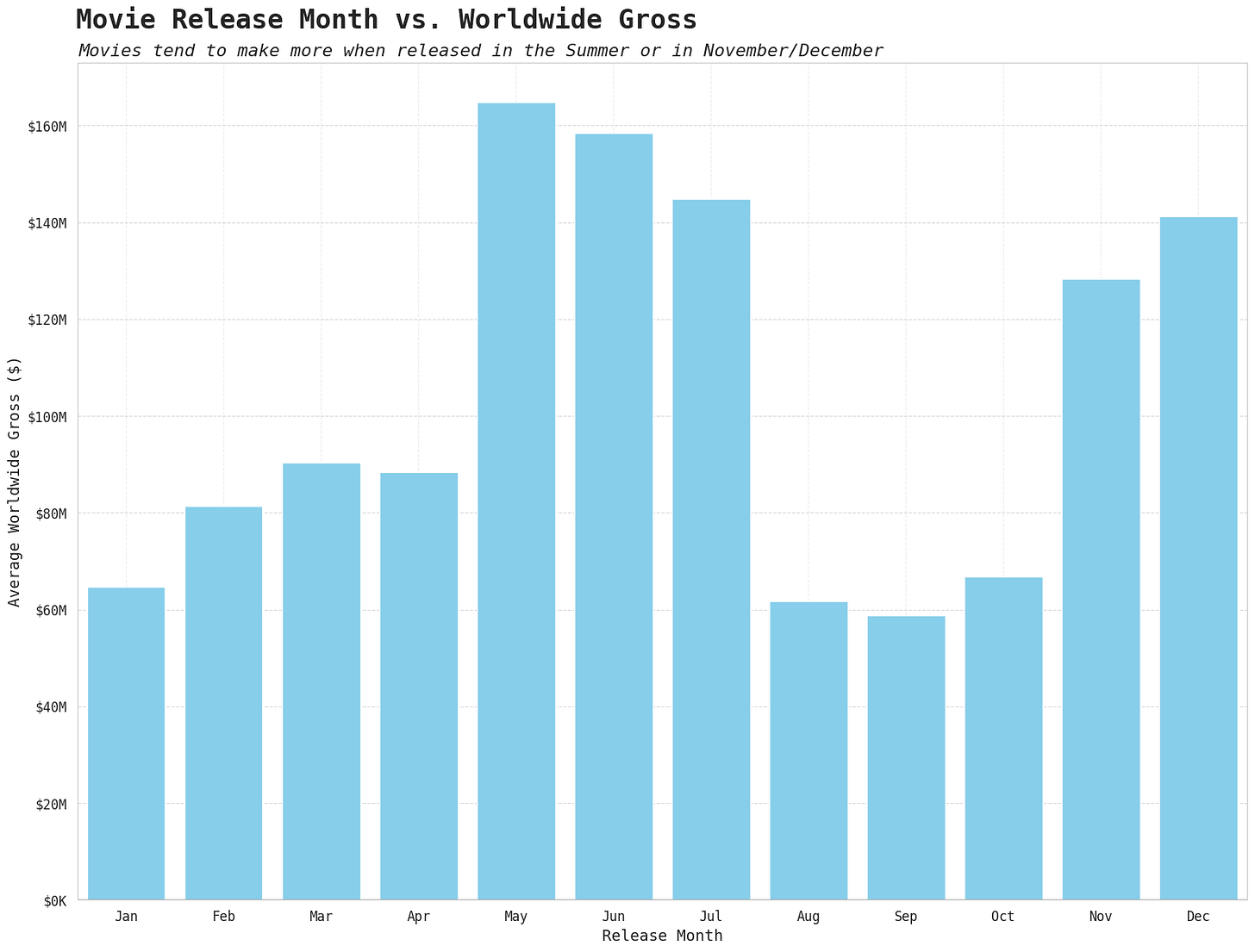
Release month would be considered a categorical variable, and the results are much more distinct. The chart below shows a clear spike in worldwide gross for films released in the Summer months, and then again in November and December. These variables would be included as dummies (i.e. a binary yes/no for each month).

I encoded some additional features to improve the model and these were:

• covid - this was a binary yes/no variable to check is a movie was released between March 2020 - December 2021 to see if it was released during the throws of lockdown

• non_us_release - another binary yes/no variable that checked if a film had any domestic US gross, if not, then it would be considered an international movie with no US release

• budget_x_year - this is an interaction term, which to describe briefly, captures the joint effect of budget and year. For example, a $100M movie released in 1990 is relatively a much larger budget than a $100M movie released today in 2025. Essentially, this should capture some of the effects of inflation

The new multivariate linear model improved accuracy, but only slightly, with now only 54% of variance explained - this tells us that production budget does the vast majority of heavy lifting when predicting worldwide gross. Looking at the findings of the model:

• Budget impact - while budget alone shows a strong positive relationship with worldwide gross (coefficient of 3.11 in our univariate model), this effect becomes negligible when accounting for other variables in our full model. This suggests that budget's apparent impact is largely mediated through other factors, particularly release year. Interestingly, the significant positive interaction between budget and release year indicates that the effectiveness of budget has improved over time, with more recent high-budget films generating better returns than older high-budget productions

• Time trends - movies in more recent years tend to earn more. But the growth isn’t linear, the rate of increase is slowing slightly

• Seasonal patterns - Summer releases have the strongest impact on worldwide gross, with movies released in May and June estimated to earn over $30M more than movies released in January, on average

• COVID effect - the pandemic had an understandably large effect on worldwide gross, with films released in that period estimated to earn $62.9M less than other films, on average

• Non-US releases - films not released in the US are predicted to earn $33M less, on average
  

---

Using the models predictions, we can look at which films performed the worst and best when accounting for all of the factors listed above.

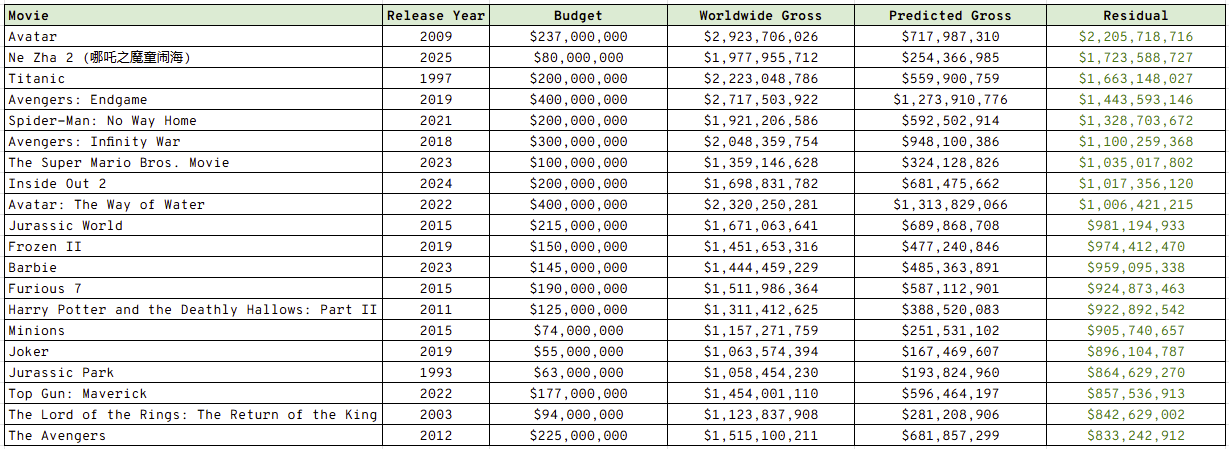
Below, are the top 20 films with the largest positive residual (difference between model predicted gross and actual gross).

Avatar, perhaps unsurprisingly, leads the way with a worldwide gross close to £3bn, whilst the model only predicted a £700m return. The budget was substantial at £237m, however the movie was wildy more successful than anticipated by the model and the industry itself.

I had never heard of Ne Zha 2 before, but it is a Chinese animated film that has been very well received critically. This only had a budget of £60m and ended up grossing almost £2bn!

The rest of the films are what you might expect, huge box office hits of familiar IPs. I am glad to see that Lord of the Rings, Titanic, and Jurassic Park making it in there - these films feel like they are from a different generation to the rest.

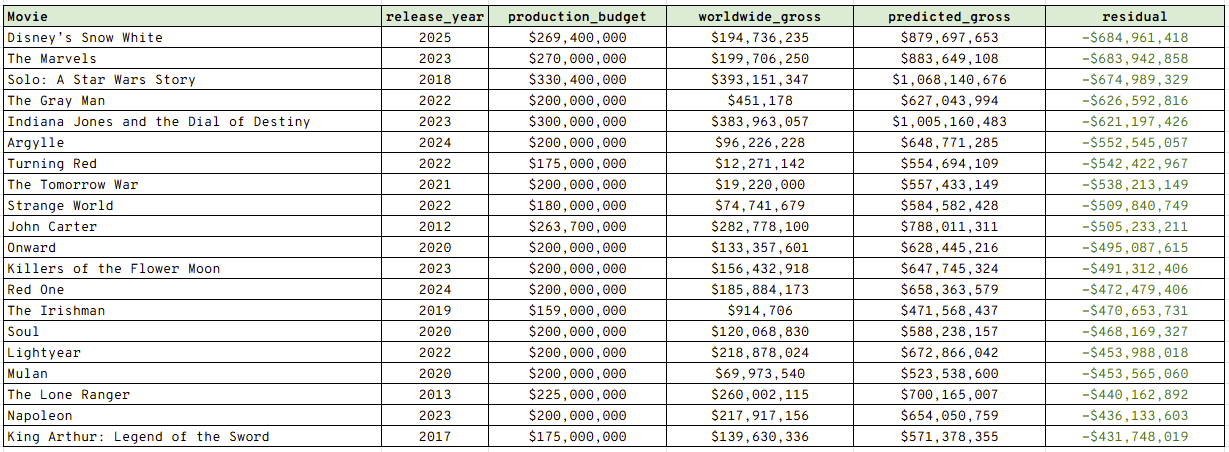
Now, we can take a look at the bottom 20! This is the top 20 films with the smallest negative residual.

Upon loading this one, I began to nod my head at the vast majority of the entries: big hollywood flops that mainly stem from recent years. There are also some perhaps unfair entries like “The Gray Man” and “The Irishman” as despite them having a small cinematic release, they were mainly streaming titles - so maybe take these two with a pinch of salt.

Snow White has been derided since coming out, I haven’t seen it so I can’t pass too much judgement, but it feels right to be leading the way, not even making its budget back.

I have never even heard of Turning Red, The Tomorrow War, Strange World, or John Carter so that also resonates.

Killers of the Flower Moon feels harsh - I really enjoyed that movie, but maybe the length and the subject matter put audiences off.

---

So, does the 10x rule stand? Not quite. However, as I put forth earlier - this analysis has considered over 6000 movies including lots of low budget and international releases, the pod covers mainly well-known films so it’s reasonable to assume that the 3.11x rule would increase when applied to a smaller and more popular sample of films.